[133. Clone Graph ] (알고리즘) bfs로 다시 풀어보기
Graph
문제
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}
Test case format:
For simplicity, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
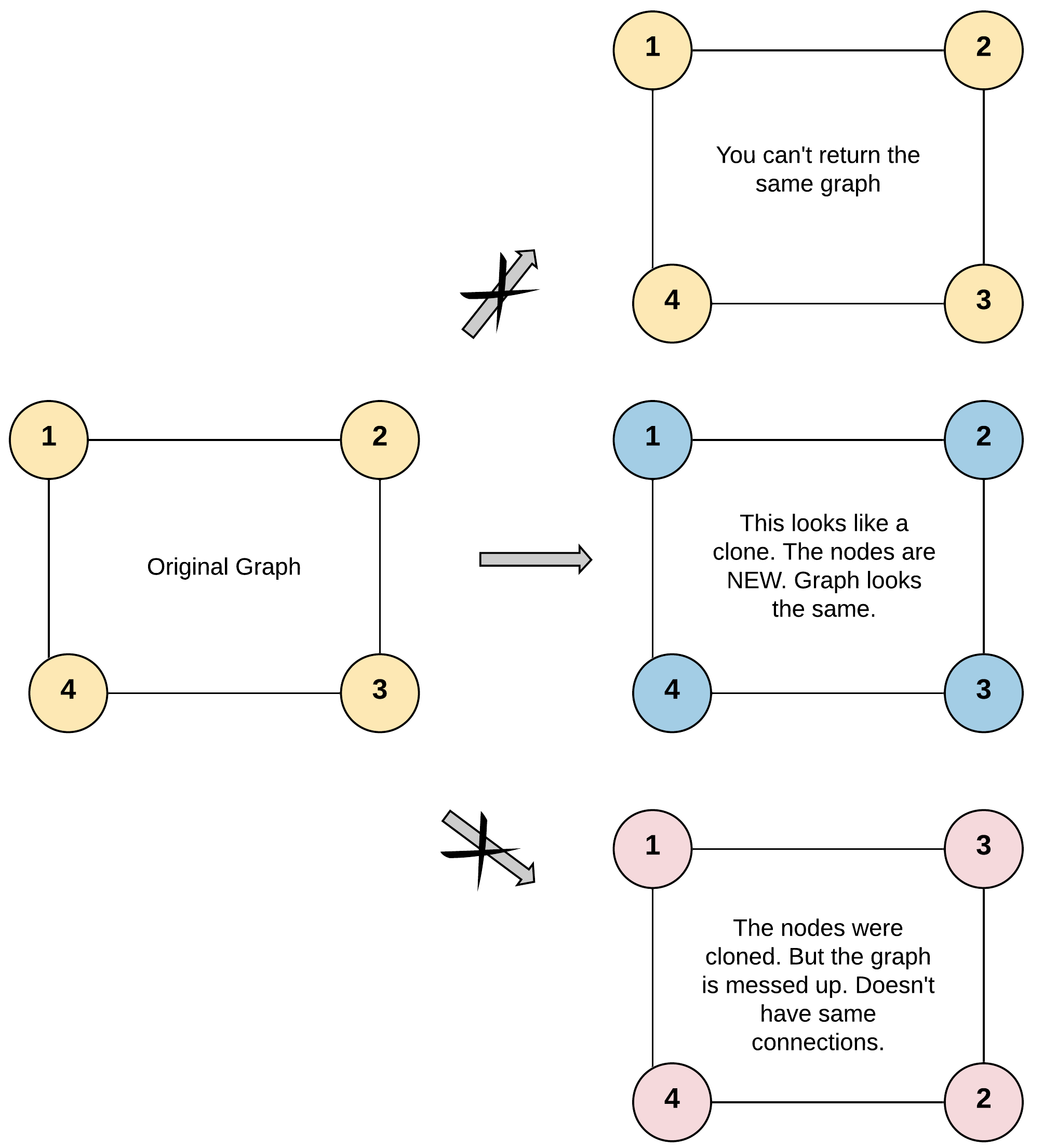
Input: adjList = [[2,4],[1,3],[2,4],[1,3]] Output: [[2,4],[1,3],[2,4],[1,3]] Explanation: There are 4 nodes in the graph. 1st node (val = 1)’s neighbors are 2nd node (val = 2) and 4th node (val = 4). 2nd node (val = 2)’s neighbors are 1st node (val = 1) and 3rd node (val = 3). 3rd node (val = 3)’s neighbors are 2nd node (val = 2) and 4th node (val = 4). 4th node (val = 4)’s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
Input: adjList = [[]] Output: [[]] Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = [] Output: [] Explanation: This an empty graph, it does not have any nodes.
Constraints:
- The number of nodes in the graph is in the range
[0, 100]. 1 <= Node.val <= 100Node.valis unique for each node.- There are no repeated edges and no self-loops in the graph.
- The Graph is connected and all nodes can be visited starting from the given node.
스스로 고민
접근법
- 그래프를 똑같이 복제하면된다.
- 근데 어떻게 해야될까 고민을 했다.
- 우선 링크드 리스트에서 한 개가 아닌 여러개와 묶여 있는 개념으로 이해하긴 했는데 처음 노드에서 다음 노드로 어떻게 이동 시켜야 할지 느낌이 안왔다.
"""
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
"""
from typing import Optional
class Solution:
def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
new_node = Node()
while node:
new_node.val = node.val
new_node.neighbors = node.neighbors
return new_node
- 이렇게 코드를 작성한다고 했을 때 다음 node로 어떻게 재귀호출 해서 이동 하면되는 걸까?
음…..응?

- 정신이 나갔었나보다.
- 말도 안되는 코드에서 여기서 이제 어떻게 해야되는지 고민하고 있었다.
- 노드를 순회하면서 복사해야되나? 아니면 복사 해놓고 순회한 내용을 넣어야되나?
머릿 속에 개념이 잡히지 않아서 열심히 구글링을 했는데 우선 그래프나 트리와 같은 자료구조를 탐색 한다는 개념있다면 DFS 나 BFS를 떠올리면 된다. (무조건은 아니지만 첫 번째로 이 개념을 떠올려보도록 노력하자)
- 탐색은 bfs, dfs!
- dfs, bfs 둘 다 잘 사용해야된다고 생각하지만 우선 하나만 잘해보자!
- dfs 부터 익숙해지면 bfs를 이용해서 지금 문제를 다시 풀어보려고 한다.
- dfs를 먼저 고른 이유는 특별한 이유는 없다. 그냥 왠지 쉬울거 같아서..?
의사코드
- 우선 dfs는 한 놈만 패는 느낌으로 깊숙히 다 찍먹하고 돌아댕기는 느낌이다.
- 그런 느낌을 코드로 어떻게 표현하면 좋을까?
- 재귀가 안성 맞춤이라고 생각한다. 조건에 만족할 때 까지 계속 패는 느낌
- 하지만 재귀를 사용할 때는 무한루프에 빠지지 않도록 항상 정신차려야 된다. 똥컴이라 비행기 이륙소리 바로 난다.
- 우선 재귀에 빠지지 않도록 방문한 노드는 다시 방문하지 않도록 기록 및 검사를 해야한다.
- 방문한 노드를 기록할 딕셔너리 선언
- dfs 함수를 만들고 첫 조건에 해당 노드가 방문한 이력이 있는지 검사를 한다.
- 방문한 이력이 있으면 재귀호출 종료
- clone이라는 변수명에 새로운 노드에 원본 노드의 벨류 값을 넣어준다.
- 이 clone은 현재 노드의 키 값으로 visited 딕셔너리에 저장시킨다.
- 현재 노드의 이웃한 노드 값들을 반복문으로 뽑는다.
- 이때 neighbors에 넣을 값들은 재귀호출로 다시 부른다.
- adjList =
[[2,4],[1,3],[2,4],[1,3]]오리지널 노드가 이와 같을 경우 복제 과정을 시각화하면 아래와 같다.

구현 코드
class Node:
def __init__(self, val=None, neighbors=None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
def cloneGraph(node):
if not node:
return None
visited = {} # 방문한 노드를 기록하기 위한 딕셔너리
def dfs(original):
if original in visited:
return visited[original]
clone = Node(original.val)
visited[original] = clone
for neighbor in original.neighbors:
clone.neighbors.append(dfs(neighbor))
return clone
return dfs(node)
-

- adjList =
[[2,4],[1,3],[2,4],[1,3]]라고 주어진다면 - 첫 번째 노드 값의 val 는 1이고 이 노드의 키워드로 visited 딕셔너리에 저장된다.
- 현재 오리지널 노드의 neighbors 는 2와 4 들어있는데 반복문에서 처음에 2가 불려 나온다.
- 해당 2의 숫자 값으로 다시 dfs가 재귀호출된다.
- 그럼 다시 2의 키 값으로 visited에 저장되고 2의 neighbors인 1과 3이 호출되는데 여기서 1이 다시 불러진다.
- 이 때 1은 이미 호출 되었으니 처음 재귀호출은 종료되고 3으로 진행되는 식이다.
시간 복잡도와 공간 복잡도
시간 복잡도:
- 각 노드는 한 번만 방문됩니다. 방문된 노드는
visited딕셔너리에 저장되므로 이미 복제된 노드는 다시 복제하지 않는다. - 그래프의 모든 노드와 간선을 탐색해야 하므로 시간 복잡도는 O(V + E)다. 여기서 V는 노드 수이고 E는 간선 수다.
공간 복잡도:
visited딕셔너리는 그래프의 모든 노드를 방문한 후에 그래프와 같은 크기의 노드와 복제된 노드를 저장하므로, 공간 복잡도는 O(V)다. 여기서 V는 노드 수다.- 재귀 호출 스택에 사용되는 공간은 DFS의 깊이에 따라 결정되며, 최악의 경우 그래프의 높이에 비례한다. 그래프가 깊다면 스택 공간도 커질 수 있다.
요약하면, 주어진 코드의 시간 복잡도는 O(V + E)이고, 공간 복잡도는 O(V)다. 이 코드는 그래프 복제 문제를 효율적으로 해결하는데 사용할 수 있다.
회고 과정
지금 코드에서 뭘 개선할 수 있지?
- 솔직히 너무 복잡하다고 생각했다.
- dfs 같은 경우 스택으로 구현이 가능하다고 해서 스택으로 다시 만들어 봤다.
from collections import deque
def cloneGraph(node):
if not node:
return None
visited = {} # 방문한 노드를 기록하기 위한 딕셔너리
def cloneNode(original):
clone = Node(original.val)
visited[original] = clone
return clone
stack = deque()
visited[node] = cloneNode(node) # 시작 노드를 미리 추가
stack.append(node)
while stack:
current = stack.pop()
for neighbor in current.neighbors:
if neighbor not in visited:
visited[neighbor] = cloneNode(neighbor)
stack.append(neighbor)
visited[current].neighbors.append(visited[neighbor])
return visited[node]
다른 사람 코드를 보고 그 기준으로 어떤 부분을 개선 할 수 있는지 최종 회고
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
from typing import Optional
class Solution:
def cloneGraph(self, node: Optional['Node']) -> Optional['Node']:
if not node:return node
d = {}
visited = set()
q = deque([node])
while q:
for _ in range(len(q)):
curr = q.popleft()
if curr not in visited:
if curr not in d:
d[curr] = Node(curr.val)
for n in curr.neighbors:
if n not in d:
d[n] = Node(n.val)
d[curr].neighbors.append(d[n])
q.append(n)
visited.add(curr)
return d[node]
해당 코드는 큐를 사용해서 그래프를 복제 구현했다. bfs 방법인데 문제를 더 많이 풀어봐야 감이 잡힐 것 같다.
댓글남기기