[2. Add Two Numbers] (알고리즘)
Linked List
문제
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:
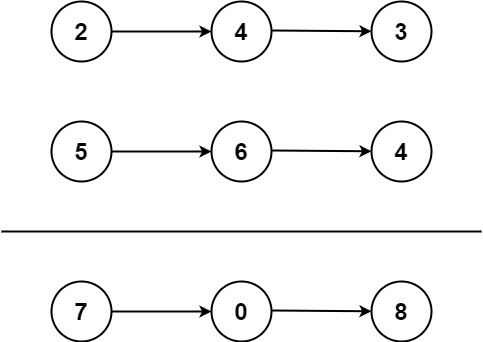
Input: l1 = [2,4,3], l2 = [5,6,4] Output: [7,0,8] Explanation: 342 + 465 = 807.
Example 2:
Input: l1 = [0], l2 = [0] Output: [0]
Example 3:
Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] Output: [8,9,9,9,0,0,0,1]
Constraints:
- The number of nodes in each linked list is in the range
[1, 100]. 0 <= Node.val <= 9- It is guaranteed that the list represents a number that does not have leading zeros.
스스로 고민
접근법
- 문제는 l1 이 2,4,3 l2가 5,6,4 하고 한다면 243 + 564 -> 708
- 708 이 값을 뒤집어서 807을 리턴해주면 된다.
의사코드
- 각 링크드 리스트가 none 값이 나올 때까지 값들을 추출해준다.
- 값을 추출해줄 때는 String으로 뽑아준다. 그래야 계산하기 편하다.
- l1 과 l2 값을 다시 int 로 바꾸고 계산한다음 링크드 리스트에 다시 넣어서 반환
구현 코드
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
a = ""
b = ""
while l1:
a += str(l1.val)
l1 = l1.next
while l2:
b += str(l2.val)
l2 = l2.next
c = int(a[::-1]) + int(b[::-1])
c = str(c)
result = None
for digit in c:
new_node = ListNode(int(digit))
new_node.next = result
result = new_node
return result
시간 복잡도와 공간 복잡도
시간 복잡도:
- 두 링크드 리스트를 순회하며 각 노드의 값을 문자열로 저장하는 데 걸리는 시간 복잡도는 O(n), 여기서 n은 링크드 리스트의 노드 수다.
- 문자열을 정수로 변환하는 작업은 O(n) 시간이 소요된다.
- 정수로 된 결과를 문자열로 변환하여 반복하며 링크드 리스트를 생성하는데 걸리는 시간은 노드 수에 비례하므로 O(n) 다.
- 따라서 전체 시간 복잡도는 O(n) 다.
공간 복잡도:
- 문자열
a,b,c는 링크드 리스트의 노드 값들을 문자열로 저장하기 위해 사용되는 공간이다. 이들 문자열의 크기는 각각 링크드 리스트의 노드 수와 관련이 있으며, 각각 O(n)의 공간을 사용한다. result링크드 리스트를 생성하는 과정에서도 링크드 리스트 노드들을 생성하여 저장하는데, 이 노드의 수 역시 n에 비례하므로 O(n)의 공간을 사용한다.- 따라서 전체 공간 복잡도는 O(n) 다.
회고 과정
다른 사람 코드를 보고 그 기준으로 어떤 부분을 개선 할 수 있는지 최종 회고
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
head = ListNode()
node = head
while l1 != None and l2 != None:
nxt = ListNode()
node.next = nxt
res = l1.val + l2.val + node.val
if res >= 10:
node.val = res - 10
nxt.val = 1
else:
node.val = res
node = node.next
l1 = l1.next
l2 = l2.next
if l1 == None and l2 != None:
while l2 != None:
nxt = ListNode()
node.next = nxt
res = l2.val + node.val
if res >= 10:
node.val = res - 10
nxt.val = 1
else:
node.val = res
node = node.next
l2 = l2.next
if l2 == None and l1 != None:
while l1 != None:
nxt = ListNode()
node.next = nxt
res = l1.val + node.val
if res >= 10:
node.val = res - 10
nxt.val = 1
else:
node.val = res
node = node.next
l1 = l1.next
curr = head
while curr.next != None:
prev = curr
curr = curr.next
if curr.val == 0:
prev.next = None
return head
주어진 코드가 더 나은 이유는 노드를 생성하고 처리하는 부분이 더 효율적으로 이루어져 있기 때문이다. 이 코드는 두 링크드 리스트의 노드를 동시에 순회하며 덧셈을 수행하면서, 새로운 노드를 생성하고 연결하여 결과를 생성한다.
이 코드의 시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity)를 살펴보겠다.
시간 복잡도:
- 주요 작업은 두 링크드 리스트의 노드를 순회하며 덧셈 연산을 수행하고, 결과 노드를 생성하는 작업이다.
- 순회하는 동안 각 노드마다 상수 시간 작업(덧셈 연산, 노드 생성 및 연결)이 이루어지므로, 두 링크드 리스트의 길이가 n이라고 할 때, 전체 작업은 O(n) 시간이 소요된다.
공간 복잡도:
- 새로운 결과 노드를 생성하고 이어붙이는 것이 주요 작업이다.
- 생성되는 노드의 수는 두 링크드 리스트 중 길이가 더 긴 링크드 리스트의 길이와 같다. 따라서 공간 복잡도는 O(max(n, m))입니다. 여기서 n과 m은 두 링크드 리스트의 길이 중 더 긴 길이를 나타낸다.
이 코드가 더 좋은 이유는 공간 효율성과 코드 구조의 단순성에 있다. 이 코드는 결과 노드를 생성하여 이어붙이는 방식으로 동작하므로, 결과를 생성하면서 중간에 계산 값을 메모리에 유지하거나 별도의 문자열 변환 과정이 필요하지 않는다. 또한 두 링크드 리스트의 길이가 다를 때에도 잘 동작한다.
- 시간을 두고 완벽하게 이해가 될 때 까지 지속적으로 체크해야될 거 같다.
댓글남기기